一次関数の応用問題(面積の問題)の解き方
2年生の一次関数の応用の問題で2つの直線とx軸またはy軸で囲まれた面積を求める問題があります。
次のような問題です。
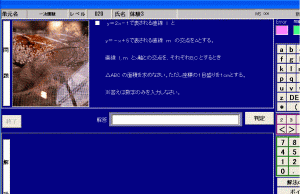
「y=2x−1 で表される直線l(エル)とy=−x+5 で表される直線mの交点をAとする。
直線l、mとx軸との交点を、それぞれB、Cとするとき
△ABCの面積を求めなさい。ただし座標の1目盛りを1cmとする。」
よくテストに宿題されます。
栄翔塾では、次のように学習します。
ヒントのボタンを押すと似た問題と解き方が表示されます。
そこで解き方を確認します。
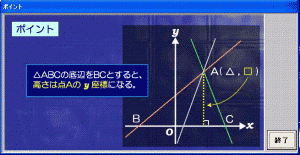
問題を解く上で役立つポイントも表示できます。
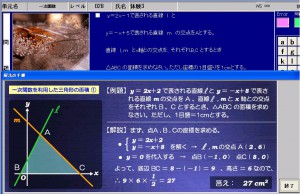
生徒には問題の一次関数を実際にグラフ用紙に描いてもらいます。
その上で、2直線の交点Aの座標を、2つの直線の式を連立方程式を解いて求めてもらいます。
その準備を経て計算です。
BとCの座標(この問題ではx座標)を、2直線の式のyに0(ゼロ)を代入することで求めます。
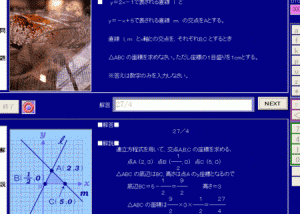
計算で求めたA、B、Cの座標が正しいかをグラフ上で確認します。
3つの座標が分かると三角形の底辺と高さが判明します。
そして、答えを入力し、判定ボタンを押すと答えの正誤が即座に判明します。
1問1問に計算の過程も画面に表示されますので、間違ったときには、間違いの原因がすぐに確認できます。
解説を見ながら、難しい問題も自力で解き易くなっています。
数学の得意な生徒はこのやり方で難しい問題のやり方もどんどん習得していきます。
一次関数の応用問題(動点の問題)の解き方
2年生の一次関数の応用の問題で動点の問題があります。
栄翔塾では、次のように学習します。
問題は次の通りです。
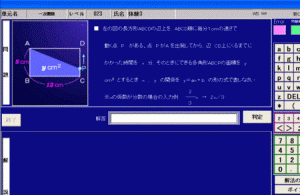
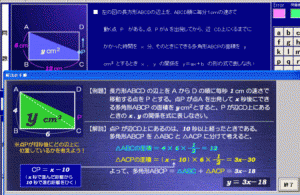
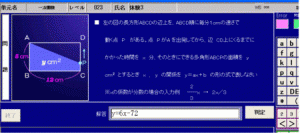
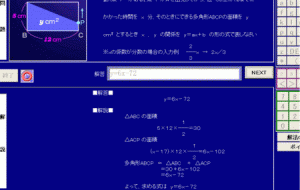
「左の図の長方形ABCDの辺上を、ABCD順に毎分1cmの速さで動く点Pがある。
点PがAを出発してから、辺 CD上にくるまでにかかった時間をx分、そのときにできる多角形ABCPの面積をycm2(平方センチメートル)とするときx、yの関係をy=ax + b の形の式であらわしなさい。」
ヒントの画面をの類題で解き方を確認します。
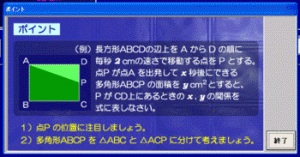
台形の面積を求めるために台形を2つの三角形に分けることにします。
ポイントは時間によって変化する三角形の底辺の長さを、時間であるx(エックス)で表すことができるかどうかということです。
底辺の長さをxであらわすことができると、解答にぐっと近づきます。
解くためのポイントも表示されます。
解答が導けたら、答えを入力します。
判定ボタンを押すと答えの正誤が即座に判明します。
1問1問に計算の過程も画面に表示されますので、間違ったときには、間違いの原因がすぐに確認できます。
解説を見ながらなので、難しい問題も自力で解くことができます。
数学の得意な生徒はどんどん進めます。
文字式の利用はハードルが高い。
2年生の数学で文字式の計算を学習します。
複数の項からなる文字式同士のたし算とひき算。
複数の項の文字式と単項式のかけ算、わり算。
そして、分母の異なる分数の文字式のたし算とひき算の計算のやり方を習得します。
その後に、文字式の変形ができるようにします。
複数の文字からなる文字式を式の中にあるどの文字でも、イコールとして表せるように練習します。
文字式を自由に計算できるようになっておくことが、その後習う連立方程式や一次関数の学習をスムーズに進めていくうえで大事です。
文字式の計算が自由にできるまで練習した後、取り組む課題は文字式の利用です。
この単元はハードルが高く、中間のテストで差がつく単元です。
「2つの自然数が2m−1、2n−1と表されるとき、2数の和は必ず偶数になることを文字式を使って説明しなさい」という問題です。
次のような式を使います。
(2m−1)+(2n−1)=2(m + n−1)
次のような問題もあります。
「2けたの正の整数と、その数の十の位の数と一の位の数を入れかえてできる数の和は、11の倍数になることを、文字式を用いて説明しなさい。」
栄翔塾では、オンリーワンというテキストを使います。
次のようにステップを踏んで学習できるようになっています。
偶数をnを用いて表せ。
3の倍数をnを用いて表せ。
10でわると7あまる数をnを用いて表せ。
十の位の数がa、一の位の数がbである2けたの数を、a、bを用いて表せ。
連続する3つの奇数を、整数nを用いて表せ。
栄翔塾では、このような種類の問題を学習しながら、文字式を利用した説明問題をできるようにしていきます。