一次関数の応用問題(動点の問題)の解き方
2年生の一次関数の応用の問題で動点の問題があります。
栄翔塾では、次のように学習します。
問題は次の通りです。
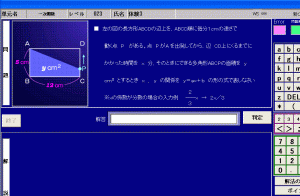
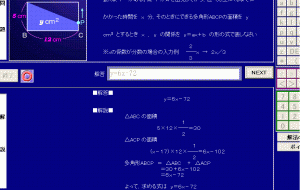
「左の図の長方形ABCDの辺上を、ABCD順に毎分1cmの速さで動く点Pがある。
点PがAを出発してから、辺 CD上にくるまでにかかった時間をx分、そのときに
できる多角形ABCPの面積をycm2(平方センチメートル)とするときx、yの関係を
y=ax + b の形の式であらわしなさい。」
(画像をクリックすると、画像が大きくなり問題が見易くなります。)
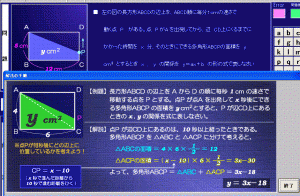
ヒントの画面をの類題で解き方を確認します。
台形の面積を求めるために台形を2つの三角形に分けることにします。
ポイントは時間によって変化する三角形の底辺の長さを、時間であるx(エックス)で表すことができるかどうかということです。
底辺の長さをxであらわすことができると、解答にぐっと近づきます。
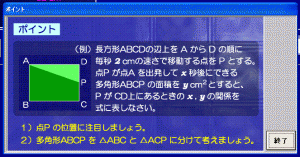
解くためのポイントも表示されます。
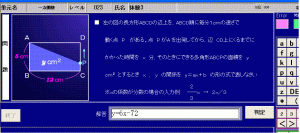
解答が導けたら、答えを入力します。
判定ボタンを押すと答えの正誤が即座に判明します。
1問1問に計算の過程も画面に表示されますので、間違ったときには、
間違いの原因がすぐに確認できます。
解説を見ながらなので、難しい問題も自力で解くことができます。
数学の得意な生徒はどんどん進めます。